 |
|
 |
|
|
|
|
|
|
|
1. The center of mass
|
|
An object's center of mass of can be described as the point at where all its mass has been concentrated and all external forces influence. For a rigid body, the center of mass location is fixed and a corporeal point belongs to the object.
It should be noted that the center of mass is not necessarily the same geometric center in an object. Center of gravity can be defined as the resultant effect point of the gravitational forces on an object. When an object is placed in a uniform gravitational field, its center of mass coincides with center of gravity. But in non-uniform gravitational fields, these two points are different and this causes a small but measurable gravitational torque. Peculiarities of a large number of particles' center of mass distributed in space and not necessarily in one plane are calculated by the following relationships:
"M" is equal to the total mass of the device.
In general, a system of particles' center of mass showed with "r" is defined as each particle's situations average (r) with the mass "m".
Or for continuous bodies:
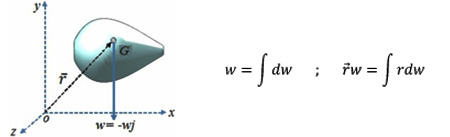
For a continuous distribution of mass with density and total mass "M", above relational will become the integral form:
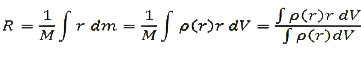
Common methods to measure center of gravity include hanging systems, single support, multi-support and spinning systems among which the rotational (spinning) system, the dynamic and the rest are categorized in the static methods bunch. To select any one of these methods relies on the form, size and weight of the workpiece and the desired accuracy in determining the center of gravity as well.
In some designs, determination of the center of gravity is counted as an introduction to set tensor of the Moment of inertia rounding CG point. Practical examples can be seen in design of the rockets controlling systems, satellite missiles, and spacecraft.
In some cases, determining the center of gravity, it is just a target to balance the vehicle. Setting the planes and ships' loads by relevant experts (loadmaster), are examples of this usage. In aerial and maritime industry, this expertise is known as adjusting balance and weight.
|
|
Back to the
top of page
|
|
|
|
|
|

|
|
|
|
2. Moment of Inertia
|
|
Moment of inertia is the amount of object resistance against normal rotation around specified axis. The Moment of inertia is also called rotational inertia. In fact, the Moment of inertia in rotational dynamics plays the role of material mass in linear dynamics.
This parameter outlines the relation between angular Momentum with angular velocity, torque with angular acceleration, and several other parameters. On the other hand, the Moment of inertia is total mass of each element of a substance that has been multiplied by its distance from the rotation axis in square.
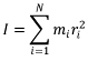
In this formula, "r" is the distance from any part of the rotation axis and "m" is the mass of each element. In constant way, the Moment of inertia is gained by the following formula that is the integral form of:
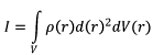
For more information, please visit the following URL:
http://hyperphysics.phy-astr.gsu.edu/hbase/mi.html
So far various methods have been developed for measuring Moment of inertia, which are all based on the relation M = Iα The important ones are torsion pendulum and rotational motion.
In the torsion pendulum method, a specific torque is applied to the object initially. Then the value α is obtained by measuring the oscillation. By putting these values in the above equation can derive the quantity of "I".
In the rotational motion method, the created angular acceleration is measured through applying constant torque to a solid object by an electric motor. The amount of applied torque is derived by measuring the electric power parameters and the value of angular acceleration is achieved by measuring the time to reach a certain "rpm". In following, some simple images related to measurement devices with mentioned methods can be seen.

In designing the system of driving force to perform the maneuvers of moving objects such as aircraft, some torques are used similar to following equations.
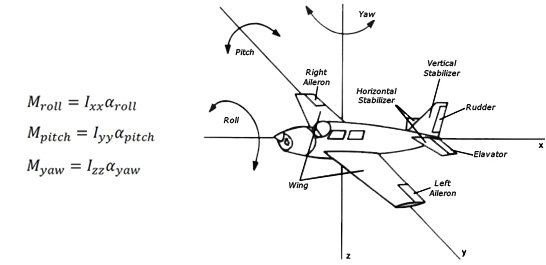
To calculate the strength of structures like the maximum allowable bending Moment on a structural steel beam, the Moment of inertia is used as second anchor and is obtained from tension formula as following:
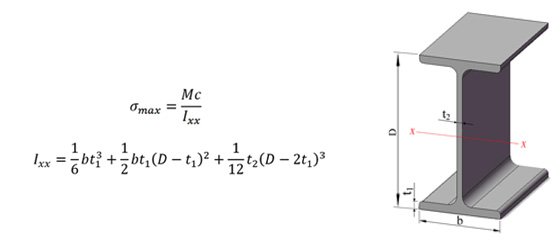
|
|
Back to the
top of page
|
|
|
|
|
|

|
|
|
|
3. Product of Inertia
|
|
In a Moment of inertia tensor that is written as follows:
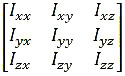
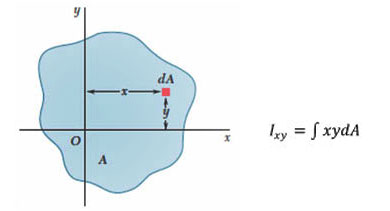
Non-diagonal elements, is called the multiplicative or Product of Inertia. Product of inertia for a rigid body is defined as:
According to the symmetry law, in above tensor Iyy, Ixy, Ixz, Iyz, Ixy and Izy are equal tow to two respectively. Unlike the original Moment of inertia, the multiplying Moments of inertia can be negative or zero. The systems of measuring the product of inertia are mostly rotational. To develop a comprehensive controlling program for rigid objects, the Moments of inertia tensor with complete parameters is needed. Also, to calculate the rotational kinetic energy, angular Momentum and required torque for rotation of a solid body with angular acceleration "α", are derived through following relations respectively:
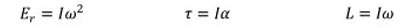
|
|
Back to the
top of page
|
|
|
|
|
|

|
|
|
|
4. Researchers and industry experts
This group is ready to share their experiences in the field of mass properties with managers and researchers working in various industries who intend to do theoretical research or joint operational projects.
|
|
Back to the
top of page
|
|
|
|
|
|

|
|
|
|
5.
Students
|
|
Undergraduate and graduate students in mechanical engineering, aerospace engineering, physics, mathematics and related fields of measurement and instrumentation systems can communicate with our experts in order to perform academic research or thesis and seminars and consequently improve their academic activities along with an idea and industrial applications. Students can also take advantage of our free consultation and technical documents. For more information, please refer to the "Contact us" panel.
|
|
Back to the
top of page
|
|
|
|
|
|

|
|
|
|
6. New Events
|
|
72nd Annual
International
Conference on Mass
Properties
Engineering
May 18-23,
2013,
St. Louis,
Missouri
http://www.sawe.org/conferences/intl13
71st
International
Conference on Mass
Properties Society
i(Download
brochure)
|
|
Back to the
top of page
|
|
|
|
|
|

|
|
|
|
7. Scientific resources, articles and technical documents
|
|
Manual users and help systems, various research papers, short notes, brochures, training movies and compact discs (CD) containing scientific and reference books (Text Book) are available at the group's office and is usable to fans and those interested in this field . For example, a number of books and articles listed below are available for download. If you're looking for something specific, please correspond with us.
To receive the full text of the Book of static and dynamic Beer Johnston (102 MB), just email us.
Quote of the content of this page is permitted if the source (www.sp.com) mentioned.
|
|
Vector Mechanics for Engineers, Beer & Johnston, Content_&_Appendix
Vector Mechanics for Engineers, Beer & Johnston, Chapter 5- Distributed Forces- Centroids and Centers of Gravity
Vector Mechanics for Engineers, Beer & Johnston, Chapter 9- Distributed Forces- Moments of Inertia
|
|
Mass Properties Measurement Handbook, Part 1
Mass Properties Measurement Handbook, Part 2
Mass Properties Measurement Handbook, Part 3
How to Calculate Mass Properties (An Engineer's Practical
Guide)
Mass Properties Measurement Errors Which Could Have Been
Easily Avoided
The
Seven Secrets of Accurate Mass Properties Measurement
Using the Moment of Inertia Method to Determine Product of
Inertia
Design of Orifice-Type Aerostatic Thrust Bearing
Guidelines for Mass Properties Control on International
Space & Missile Systems
Mass Properties Management and Control for Military Aircraft
Standard Coordinate Systems for Reporting the Mass
Properties of Flight Vehicles
Weight and Balance Data Reporting Forms for Guided Missiles
and Space Launch Vehicles
Weight Control Technical Requirements for Surface Ships
Mass Properties Control for Space Vehicles
|
|
Back to the
top of page
|
|
|
|
|
 |
|
 |
|
|
|
|
|
|
|
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;